﹅ 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
모든 노드에서 다른 모든 노드까지 가는 최소비용
- start → mid → end
표[2차원 배열]를 만들어 중간 경유지에 따라 값을 계속 갱신시킨다.
시간복잡도 : O(V^3)
다익스트라 : 한 노드 → 다른 모든 노드, O(ElgV)
플로이드 워셜 알고리즘은 다익스트라 알고리즘과는 달리 "모든 노드 쌍" 에 대해 최단거리를 구하고,
음의 가중치를 가지는 그래프에서도 쓸 수 있다는 것이 특징이다.
💡 그래프 알고리즘에 대해 읽어볼 좋은 글
https://yozm.wishket.com/magazine/detail/2411/
﹆ 작동 원리

1 → 4 로 바로 가는 방법은 존재하지 않지만, 중간 노드 mid 를 3으로 둔다면, 1 → 3 → 4 로 가는 최단 경로가 생긴다.
플로이드 워셜 알고리즘의 핵심은 start → mid → end
기본이 되는 표는 아래와 같이
- 1 → 1 본인에서 본인으로는 갈 수 없으므로 0을 넣어준다
- 나머지는 INF 로 넣어준다 (아직 어느 수가 들어갈지 모르기 때문)
| 1 | 2 | 3 | 4 | |
| 1 | 0 | ♾️ | ♾️ | ♾️ |
| 2 | ♾️ | 0 | ♾️ | ♾️ |
| 3 | ♾️ | ♾️ | 0 | ♾️ |
| 4 | ♾️ | ♾️ | ♾️ | 0 |
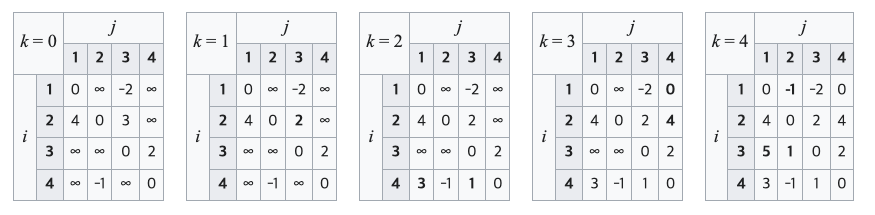
k = 0 (mid : 경유 x)
1 → 3 으로 가는 최단거리는 -2 이다.
따라서 char[A][B] = -3 넣어준다.
... 반복
k = 1 (mid : 경유 1)
2 → 1 → 3 : 1을 경유하는 경우 4 + (-2) = 2
... 반복
k = 2 (mid : 경유 2)
4 → 2 → 1 : 2를 경유하는 경우 -1 + 4 = 3
k = 3 (mid : 경유 3)
...
k = 4 (mid : 경유 4)
...
char[start][end] = Math.min(char[start][end], char[start][mid] + char[mid][end])
start : 4, mid: 2, end: 1 이라고 할 때,
2 을 경유하기 전까지, 4 → 1 는 Infinity 였다.
2 을 경유하면 4 → 2 → 1 는 -1+4 = 3 이다.
따라서 char[4][1] 은 Math.min(Infinity, 3) 의 결과인 3이 된다.
🧊 단순히 반복문을 3번 중첩시키기만 하면 되기 때문에 큰 어려움 없이 간결하게 구현할 수 있다. 단, 유의하여야 할 점은 for문에서 가운데 노드(m)가 제일 위에 있어야 한다는 점이다.
노드 j 에서 노드 i 로 가는 비용 배열 만들기
초기값 INF간선의 값을 비용 배열에 반영
모든 노드에 대해 해당 노드 거쳐서 가서 비용 작아질 경우 값 갱신
﹆ 코드
function Floyd_Warshall() {
for(let m=1; m<=N; m++) {
for(let s=1; s<=N; s++) {
for(let e=1; e<=N; e++) {
if (d[s][e] > d[s][m] + d[m][e]) {
d[s][e] = d[s][m] + d[m][e];
}
}
}
}
}
﹅해당 알고리즘 문제 : 백준 11404
https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net


문제 풀이 => https://eonhwa-theme.tistory.com/179
[백준-Gold4] 11404 플로이드 - javascript
https://www.acmicpc.net/problem/11404 11404번: 플로이드 첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다.
eonhwa-theme.tistory.com
'자료구조+알고리즘 > 알고리즘' 카테고리의 다른 글
| [DataStructure] 시간복잡도와 공간복잡도 (1) | 2024.12.15 |
|---|---|
| DP : Dynamic Programming (동적 계획법) (0) | 2024.03.26 |
| [javascript] BFS (0) | 2024.03.26 |
| DFS 와 BFS 개념정리 (0) | 2021.10.30 |

